Dante Electronics & Pc

Energia Potencial.-


Se dice que un objeto tiene energia cuando está en movimiento, pero también puede tener energia potencial, que es la energia asociada con la posición del objeto.

Energia Potencial, ejemplo: un pesado ladrillo sostenido en alto tiene energia potencial debido a su posición en relación al suelo.


Tiene la capacidad de efectuar trabajo porque si se suelta caerá al piso debido a la fuerza de gravedad, pudiendo efectuar trabajo sobre otro objeto que se interponga en su caída. 

Un resorte comprimido tiene energia potencial.


Por ejemplo, el resorte de un reloj a cuerda transforma su energia efectuando trabajo para mover el horario y el minutero. 

Energia Potencial Gravitacional


 

 El ejemplo mas cotidiano de energía potencial es la energía potencial gravitacional.

Se define la energía potencial (EP) gravitacional de un objeto de masa m que se encuentra a una altura y de algún nivel de referencia como:





EPG = mgy
 g es la aceleración de gravedad





Esta definición es totalmente compatible con la definición de trabajo por cuanto el trabajo necesario para elevar la masa m desde el nivel de referencia hasta la altura y es Fy = Peso•y = mgy.


El objeto ha acumulado una energía mgy.

Si dejamos que el objeto de masa m caiga libremente bajo la acción de la gravedad sobre una estaca que sobresale del suelo, efectuará un trabajo sobre la estaca igual a la energía cinética que adquiera llegando a ella.

Esta energía cinética puede calcularse mediante la ecuación cinemática vf2 = vi2 + 2gy.


Como vi = 0, vf2 = 2gy.


La energía cinética justo antes de golpear la estaca es ½mvf2.


Reemplazando vf2 por 2gy se obtiene ½ m•2gy = mgy. 

O sea, para elevar un objeto de masa m a una altura y se necesita una cantidad de trabajo igual a mgy y una vez en la altura y, el objeto tiene la capacidad de efectuar trabajo igual a mgy.

Notemos que la EPG depende de la altura vertical del objeto sobre algún nivel de referencia , en el caso de este ejemplo, el suelo.

El trabajo necesario para elevar un objeto a una altura y no depende de la trayectoria que se siga .


O sea, la trayectoria puede ser vertical o en pendiente u otra y el trabajo para subirlo será el mismo.

Igualmente, el trabajo que puede efectuar al descender tampoco depende de la trayectoria.

¿Desde qué nivel medir la altura y?

 Lo que realmente importa es el cambio en energía potencial y escogemos un nivel de referencia que sea cómodo para resolver determinado problema.


Una vez escogido el nivel, debemos mantenerlo en todo el problema.


 

Campo gravitatorio terrestre




Llamaremos campo gravitatorio a la perturbación que un cuerpo produce en el espacio que le rodea por el hecho de tener masa.



Podemos considerar una partícula de masa M que perturba el espacio que le rodea, creando un campo gravitatorio. 

Dicho campo se hace evidente cuando una partícula testigo de masa m se sitúa en él a una distancia r del centro de M y es atraída con una fuerza:

F = -G.(M.m/r²).uT

donde:

r = R + d

Estaremos fuera del campo gravitatorio cuando F = 0. 

Para ello r debe ser ∞. Esto es teórico. Si las masas son pequeñas en relación a la distancia la F ® 0. Ej: Tiza- bolígrafo

Intensidad del campo gravitatorio


La fuerza depende de la cantidad de masa m. 

Vamos a definir una característica del campo que solo dependa de la masa que origina el campo M y la distancia al punto que consideremos.

La intensidad del campo gravitatorio, g, en un punto del espacio es la fuerza que actuaría sobre la unidad de masa situada en ese punto. 

Su unidad es N/kg. 

Frecuentemente se usa el término campo gravitatorio para designar la Intensidad de campo gravitatorio.



Para determinar el campo gravitatorio creado por una masa puntual M situamos una masa de prueba m en un punto P del espacio a una distancia R de la masa M. 

Calculamos la F por unidad de masa

g = F/m = (-G.M.m/r²).ur/m = (-G.M/r²).ur

Podemos decir que el campo gravitatorio tiene las siguientes propiedades:



	
Es un campo central y disminuye con el cuadrado de la distancia.


	
El signo negativo es porque g y ur tienen sentidos contrarios. Las fuerzas gravitatorias siempre son atractivas




Podemos escribir la ecuación de la intensidad como F = m.g.

Esto coincide con P = m.g.

En la superficie de la Tierra g0 = (-G.M/RT²).ur

Ejemplo:

Calcula el campo gravitatorio creado por el sistema de la figura en el punto P.

Determina el módulo de la fuerza gravitatoria que actúa sobre una masa m = 0,5 kg colocada en el punto P.



u1 = -j

u2 = -i

g1 = -G.(M1.r1²).u1 = -6,67.10-11.5.106/(3.104)² = -3,7.10-13.u1 N/kg

g2 = -G.(M2.r2²).u2 = -6,67.10-11.6.106/(5.104)² = -1,6.10-13.u2 N/kg

g = g1 + g2 = 1,6.10-13i + 3,7.10-13j



F = m.g = 0,5.4,03.10-13 = 2,0.10-13 N

El campo gravitatorio se visualiza a través de unas líneas imaginarias que se llaman líneas de fuerza. 

Son la trayectoria que seguiría la unidad de masa dejada en libertad dentro del campo gravitatorio.



Así también puede definir la intensidad de campo.

uds unidad de superficie.

Intensidad de campo es el número de líneas que atraviesan la uds colocada perpendicularmente a dichas líneas

Si suponemos que la causante está en el infinito con respecto al observador: 





	
Pueden considerarse las líneas paralelas en el cilindro


	
IA= IB




Flujo del campo gravitatorio (Φ)


Es el número de líneas que atraviesan una región del espacio.



Tenemos un campo gravitatorio g, que atraviesa una superficie S, que podemos caracterizar por un vector S, perpendicular a la superficie y de módulo su área.

(Esto es la interpretación geométrica del producto vectorial)

Se define el Φ del campo gravitatorio como:

Φ = g.S = g.s.cos θ.

Si g y S son perpendiculares no hay flujo.

Teorema de Gauss


Gauss definió un Teorema para calcular el flujo del campo electrostático. 

Para el campo gravitatorio se usa una modificación de este.



Sea M una masa puntual encerrada en una esfera de radio r.

El flujo es Φ = g.S = g.s.cos 180° = - g.S

Si M está en el centro de la esfera g = -G.M/r²

Como S = 4 π r² ® Φ = -G.(M/r²).4.π.r² = -4.π.G.M

M es la masa encerrada dentro de la superficie

“El flujo del campo gravitatorio a través de una superficie cerrada es el producto de una constante. 

(- 4.π.G) por la masa encerrada dentro de la superficie”.

Mediante el Teorema de Gauss puede justificarse que una esfera homogénea se comporte en su exterior como una masa puntual situada en su centro. 

Basta con elegir una esfera concéntrica de radio r y suponer que el campo gravitatorio es cte y perpendicular a la superficie de la esfera elegida.



Tª Gauss Φ = -4π.G.Minterior Definición de Φ; Φ = -g.S = -g.4.π.r².

Igualando g = G.Minterior/r²

 



 

Principio de superposición




Se ha comprobado -también experimentalmente- que las fuerzas eléctricas se comportan en forma aditiva, es decir; la fuerza eléctrica sobre una carga q, debida a un conjunto de cargas  es igual a la  suma de las fuerzas que , que cada carga qi,ejerce separadamente sobre la carga q, es decir



en que las fuerzas  estan dadas por




En la ecuación anterior las cargas qi ocupan las posiciones dadas por los vectores  () y la carga q está en el punto . 

El principio de Superposición es conocido también como la 'regla del paralelogramo de fuerzas'.






a) 

b) 



V = 

Es un sumatorio algebraico. Cada carga va con su signo





Superficies equipotenciales







Son superficies que en todos sus puntos tienen el mismo potencial.



Si r = cte y ε = cte entonces V = cte. Todas las superficies equipotenciales son esféricas (Si solo hay una carga)





Propiedades

a) Dos superficies equiescalares no se pueden cortar.

b) El trabajo para desplazar una carga dq a lo largo de una superficie equipotencial es 0.

dW = dq (V1-V2)  V1=V2® dW = 0

c) El campo eléctrico ( vector campo ) es perpendicular en todos su puntos a una superficie equipotencial.

dW = F.dr = dq.E.dr.cos α.

Por propiedad b) el W = 0




0 =
dq•E•dr•
cos α
® cos [Ey.dr] = 0 y por tanto E perpendicular a dr


#0
= 0





Campo, potencial y carga en el interior de un conductor cargado en equilibrio eléctrico y en su superficie.







Como ya vimos, el campo en el interior de un conductor en equilibrio debe ser 0, ya que si no fuera así sus cargas no estarían en reposo, no estaría en equilibrio. Toda la carga está en su superficie. E = 0.

Potencial V1-V2= E•d = 0 ® V1 = V2

Esto es porque V1- V2 = E•d = 0





Todos los puntos del conductor cargado y en equilibrio están siempre en el mismo potencial. Si  todos los puntos están al mismo potencial, la superficie es equipotencial.

Carga







Tomamos en el interior una superficie gaussiana.

Por definición Φ = E.S´ = 0.S´ = 0

Por Gauss Φ =  ® ∑q = 0





Luego la carga no está dentro, toda está en la superficie.






Definimos una nueva magnitud.

Densidad superficial de carga σ = q/s. Carga por unidad de superficie.

También existe la carga por unidad de longitud λ = q/l.




Si el conductor es esférico y se carga la σ sería cte por simetría.




Si el conductor no es esférico la carga no se reparte por igual, hay acumulaciones en las puntas. Esto se conoce como efecto puntas. En esto se basa el pararrayos.

Otra nueva magnitud que relaciona la carga y el potencial es la capacidad C = q/V. Depende solo de sus características geométricas. Unidad Faradio (F).





Para una esfera 

Campo en un punto infinitamente próximo a un conductor cargado y en equilibrio. Teorema de Coulomb


E = σ/ε "El campo en un punto infinitamente próximo es igual a σ entre la constante dielectrica (ε)  del medio que envuelve al conductor".






Colocamos sobre la superficie ds`una superficie gaussiana, un cilindro.

Φ = (ds") = 0. Está en el interior del conductor.

Φ = (lateral) = 0. No atraviesan las líneas de fuerza lateralmente al cilindro.





Solo hay Φ por ds.

Eds= dq/ε ® E = dq/ε.ds = σ/ε

Por definición de flujo ® dΦ = E.ds = E.ds.cos α = E.ds

Por Teorema Gauss dΦ = dq/ε

Esto ocurre siempre que E es perpendicular a dS`

Esto sirve para un condensador plano






Líneas paralelas E = cte.

En los terminales el campo se curva pero suele despreciarse.








Campo creado por un plano infinito cargado uniformemente
Campo creado por una distribución esférica de carga en el exterior



- El plano cargado se caracteriza por su densidad superficial de carga constante σ = Q/S.

- Por simetría, las líneas de campo son paralelas entre sí y perpendiculares al plano.

- Elegimos como superficie de Gauss, SG, un paralelepípedo perpendicular al plano.

- Calculamos el flujo eléctrico a traves de SG. Sólo contribuyen al flujo eléctrico las caras paralelas al plano: S1 y S2. El flujo a traves de las otras caras es nulo porque E y dS son perpendiculares.

Φ = ∫SG E.dS = ∫S1 E.dS + ∫S2 E.dS

Φ = E.S1 + E.S2 = 2.E.S

- Aplicamos el teorema de Gauss:

Φ = Q/ε0; 2.E.S = Q/ε0



El campo eléctrico creado por un plano infinito de carga es uniforme.

- La esfera, de radio R, tiene una carga Q distribuida uniformemente.

- Por simetría, el campo es radial y sólo depende de la distancia r al centro de la esfera.

- Elegimos como superficie de Gauss SG una esfera concéntrica con la distribución de carga, de radio r > R.

- Calculamos el flujo eléctrico a traves de SG. Sobre la superficie de Gauss el campo eléctrico E tiene módulo constante y dirección paralela a dS.

Φ = ∫SG E.dS = ∫S1 E.dS = E.SG = E.4.π.r²

- Aplicamos el teorema de Gauss:

Φ = Q/ε0; E.4.π.r² = Q/ε0



El campo eléctrico creado por una distribución esférica de carga en un punto exterior es el mismo que crearía una carga puntual Q situada en el centro de la esfera.





Potencial creado por una esfera uniformente cargada en el exterior.

• dW = F.dr = q.E.dR = q.E.dR	E.dR = V1 – V2
  dW = -ΔEp = (V1 – V2).q

• 

El punto 2 me lo llevo al ∞.

• 

El potencial creado por la esfera es como si la carga estuviera en el centro de la esfera.

En un punto interior y en la superficie.








VA = 
 Demo anterior con R = r


EB = 0
VB = VA =  Superficies equipotenciales

Momentos y productos de inercia

Se define momento de inercia de un sistema respecto a un eje, plano o punto como la suma de las masas de las partículas por los cuadrados de las distancias a dichos elementos geométricos. Los elementos (, , ) de la diagonal principal de la matriz son los momentos de inercia respecto a los ejes , y .

Se define producto de inercia de un sistema respecto a dos planos como la suma de las masas de las partículas por el producto de las separaciones a ambos planos. Se considera que la separación a un plano es positiva a un lado del plano y negativa al otro. Los elementos (, , ) fuera de la diagonal principal de la matriz son menos los productos de inercia respecto a los pares de planos formados entre , y . Se tiene:

En general, es necesario recurrir al calculo integral para calcular los momentos y productos de inercia de solidos. Sin embargo, las siguientes relaciones, llamadas relaciones fundamentales (obvias si uno considera los ejes de coordenadas y planos perpendiculares a ellos por el origen) facilitan frecuentemente el cálculo:

1. El momento de inercia respecto a un eje es la suma de los momentos respecto a dos planos perpendiculares que se cruzan en él.
2. El momento de inercia respecto a un punto es la suma de los momentos respecto a tres planos perpendiculares que pasan por él.
3. El momento de inercia respecto a un punto es la semisuma de los momentos respecto a tres rectas perpendiculares que pasan por él.
4. El momento de inercia respecto a un punto es la suma de los momentos respecto a un plano que pasa por él y respecto a una recta perpendicular al plano y que pase por él.
5. Los productos de inercia son nulos si uno de los dos planos es un plano de simetría.

Movimiento relativo: Generalidades

En Física, dado que los observadores en general están en movimiento unos respecto de otros, es importante determinar como hay que expresar las relaciones de las magnitudes en consideración en diferentes sistemas de coordenadas que están, en general, moviéndose uno respecto de otros. En este capítulo de la cinemática nos interesamos, por tanto, en ver como se relacionan las magnitudes (posición, velocidad y aceleración) expresadas en diferentes sistemas de coordenadas.

El esquema general del problema lo podemos fijar observando el dibujo, que muestra un sistema de referencia que suponemos fijo (X,Y,Z) y otro que se supone en movimiento respecto de él (X’,Y’,Z’).

De la figura se deduce inmediatamente que

Derivando sucesivamente respecto del tiempo tenemos que

y

 

La evaluación de estas expresiones la vamos a realizar a partir de casos particulares sencillos, para finalmente llegar a una expresión general.

Movimiento relativo de traslación uniforme.

Supongamos primero que los sistemas de referencia O y O’ se mueven el uno respecto del otro con velocidad constante y de modo que los ejes mantienen continuamente sus orientaciones relativas. Más aún, supongamos que los ejes X y X’ son colineales y los ejes Y e Y’ y Z y Z’ son paralelos, de tal manera que un sistema de referencia se mueve respecto del otro con una velocidad constante en módulo que denotamos por .

Si suponemos, por simplicidad que en t=0 los orígenes coincidían tenemos que podemos expresar la relación entre r y r’ como

es decir, expresándolo en componentes

Si añadimos a estas ecuaciones

Ya que se ha dicho antes que en Mecánica Clásica se supone el tiempo absoluto, esto es, independiente del sistema de referencia, se tienen lo que se llaman las transformaciones de Galileo, y que son la expresión de como pasar de un sistema de referencia a otro en el caso de traslación uniforme.

Derivando las ecuaciones respecto del tiempo para encontrar la velocidad tenemos:

y

Derivando la ecuación entre r y r’ tenemos entonces que

Que muestra la relación entre las velocidades en los sistemas de referencia con y sin primas(‘).
Derivando la expresión anterior para obtener la velocidad se tiene

Que muestra que la aceleración medida por uno y otro observador situado en cada uno de los sistemas de referencia es la misma.

Movimiento relativo de rotación uniforme.

Consideremos ahora dos sistemas de referencia con un origen común que giran con una velocidad angular uno respecto de otro.

Resulta claro del dibujo que la posición de cualquier punto viene descrita por r o r’, que resultan ser el mismo vector

Aunque cada uno de ellos se expresa en su sistema de coordenadas.

siendo claro por lo anterior que

Derivando en esta ecuación respecto del tiempo tenemos

(*)

donde es importante notar que al girar los vectores unitarios del sistema en movimiento respecto es preciso contemplar sus derivadas temporales, lo que da origen a los tres últios términos.

Para evaluar las derivadas de los vectores unitarios, que simplemente iran sin cambiar su tamaño, recordemos que vimos que

y por tanto en el sistema móvil

Esto es válido para todos los vectores. En particular para los vectores unitarios se tiene

Luego podemos poner

(*)=

y sustituyendo en la derivada respecto del tiempo de

Esta es la expresión que relaciona las velocidades en uno y otro sistema de coordenadas.

La Aceleración.

Derivando la velocidad tenemos lo siguiente

Por otro lado,derivando en la expresión hallada para la relación de las velocidades en uno y otro sitemas de coordenadas tenemos

Como es constante frente al tiempo

Veamos pues como calcular la

(**)

Las derivadas de los vectores unitarios las hicimos arriba , de modo que

(**)=

y por tanto

Sustituyendo las ecuaciones y en tenemos finalmente

En muchas ocasiones lo que nos interesa es conocer la cuando conocemos . Entonces la fórmula a usar es

Donde hemos hecho uso de que en este caso (movimientos sólo de rotación)

El término se denomina aceleración de Coriolis y como veremos tiene mucha importancia en una serie de situaciones habituales en la superficie de la Tierra.

El término se denomina aceleración centrífuga y tiene así mismo mucha importancia práctica.

Movimiento relativo en el caso general.

Una vez vistos los casos particulares de traslación y rotación no es difícil convencerse que el caso general puede obtenerse simplemente de permitir en nuestras expresiones que tanto como puedan depender del tiempo. Fácilmente se obtiene entonces que

y

Donde los dos términos adicionales dan cuenta de la posible dependencia de y respecto del tiempo.

CINEMÁTICA DEL CUERPO RÍGIDO
1 – Algunos de los cuerpos de la figura no son rígidos. Encuéntrelos.

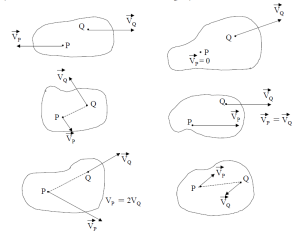
2 – Preguntas:
i) ¿Qué dirección debe tener el vector QPvvrr− (velocidad relativa de P respecto de Q) para que no cambie la distancia entre P y Q?.
ii) La expresión QPQPrvvrrrr×Ω=−, ¿satisface esa condición?.
3 – Indique la velocidad de rotación del triángulo en los tres siguientes casos: t = 0t = t1t = t4t = Tθt = 0t = t1t = t4t = Tθt = 0t = t1t = t4t = Tθ

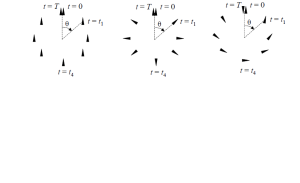
Compare con . θ&
4 – Pregunta: Si quisiera definir un ángulo tal que su derivada respecto del tiempo coincida con Ω (salvo un signo), ¿cómo lo definiría?.
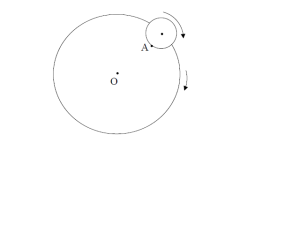
5 – El centro de una esfera describe un movimiento circular uniforme de velocidad angular ω alrededor de un punto O. Simultáneamente la esfera gira sobre sí misma, de tal forma que un punto A de la misma demora un tiempo τ en volverse a enfrentarse con el punto O (ver figura). OA
i) Encuentre la velocidad de rotación de la esfera.
ii) ¿ Cuánto tiempo transcurre entre dos pasajes sucesivos del punto A por el extremo inferior de la esfera ?.
iii) Si el eje de la Tierra fuera perpendicular a la eclíptica, ¿cuál sería el valor de Ω para la Tierra?.

6 – El eje instantáneo de rotación es el conjunto de puntos que tienen velocidad nula en un dado instante.
i) Demuestre que, si existe, es una recta paralela a Ωr.
ii) Demuestre que si hay un punto P del cuerpo tal que 0≠Ω⋅rrPv, entonces no hay eje instantáneo de rotación.
7 – Demuestre que si un punto O pertenece al eje instantáneo de rotación, entonces Pvr es perpendicular a OPrr.
8 – Teniendo en cuenta el resultado del problema 7:
i) Invente un método gráfico para determinar la posición del eje instantáneo de rotación, en los siguientes casos:
VQVPPQVQVPQPΩΩ

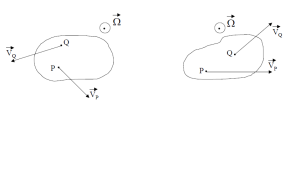
ii) Dibuje el campo de velocidades de un cilindro que rueda sin deslizar sobre un plano horizontal.
iii) Encuentre el eje instantáneo de rotación en los ejemplos del problema 3.
9 – La velocidad angular de un cuerpo rígido sometido a un movimiento rototraslatorio es (0,0,ω) y la velocidad de uno de sus puntos P es (vx,vy,0).
i) Determinar por consideraciones de cálculo vectorial, si existe un eje instantáneo de rotación.
ii) Idem que i), pero con = (vPvrx,vy,vz) con 0≠zv.
iii) ¿Cuál es, en ambos casos, el lugar geométrico de los puntos de velocidad mínima (en módulo)?.
10 – Los discos de la figura (R = 10 cm) tienen movimiento plano. Halle: 20 cm/s10 cm/sP20 cm/s20 cm/sP20 cm/s20 cm/sPP10 cm/s210 cm/s

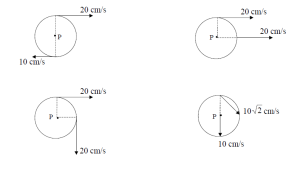
i) La posición del eje instantáneo de rotación.
ii) El vector Ωr.
iii) La velocidad del punto P.
11 – Un cilindro de radio R = 10 cm rueda sin resbalar sobre un plano horizontal. Su centro se desplaza con velocidad vC = 10 cm/s. Para los puntos P (periférico), Q (a distancia R/2 del centro) y A (sobre una manivela de longitud 2R fija al cilindro):

i) Hallar el vector velocidad en función del tiempo.
ii) Dibujar la hodógrafa correspondiente (vy vs. vx).
iii) Graficar el módulo de la velocidad en función del tiempo.
iv) Graficar las componentes vx y vy en función del tiempo. yx

Problemas aplicados a «Cinematica de Cuerpos Rigidos» y «Energia Cinetica Rotacional»:

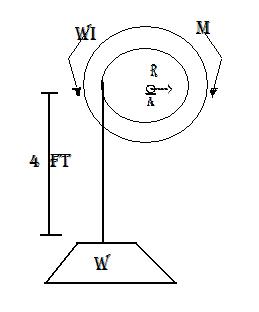
5.- Un bloque de 250 lb se suspende de un cable inextensible que esta enrollado alrededeor de un tambor de 1.25 ft de radio, unido rigidamente a un volante.

El tambor y el volante tiene un momento de inercia por combinado de I=10.5 lb ft/seg^2. en el instante mostrado la velocidad del bloque es de 6 ft/seg dirigido hacia abajo. si el cojinete A esta mal librado y la friccion en el mismo es equivalente a m por M de 60 lb ft magnitud.

Determine la velocidad del bloque despues de que este se ha movido 4 ft hacia abajo.

Solucion :

Datos:
r = 1.25 ft
I = 10.5 Lb.ft/seg²
M=60 Lb.ft
V = 6 ft/seg

Formulas:
Momento de torsión =Ť = I ∙ α
α=Ť/I
Vf ² = V0² + 2a(Xf-Xi)

Solucionando el problema:
Ť = I ∙ α
α=Ť/I     –> (60 Lb∙ft) / (10.5 Lb∙ft/s²) = 5.71 rad/seg²
at =  r ∙ α  = ( 1.25 ft ) x ( 5.71 rad/s² ) = 7.14 ft/seg²
Vf ² =  V0² + 2a(Xf – Xi)
Vf ² =  6² + 2(7.14) (4-0) = 93.12 ft/seg
Vf = √(93.12) = 9.65 ft/seg

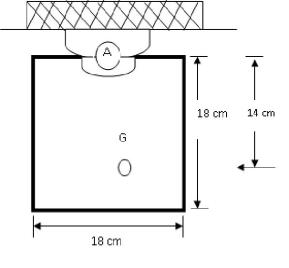
6.- Una bala de 0.05 lb se dispara con una velocidad horizontal de 1500 ft/seg contra el costado del panel cuadrado suspendido de 20 lb de una bisagra en A. Panel inicialmente en reposo.

Determine:

a) La velocidad angualar del panel.

b) Lareaccion impulsiva en A suponiendo que la bala queda incrustada en 0.0006 seg.

Solucion:

Conversiones:

1 ft =30.5 cm

X= 18 cm

X= 0.6 ft

1 ft= 30.5 cm

X= 14 cm

X= 0.4590 ft

m = w/g = 20 lb / 32 .2 =0.62 lb-masa

I = 1/12 ∙m (a²  + b² )à 1/12 ∙ (0.62) (0.6² + 0.6²)

I = 0.0372 lb ft

a) v=r∙ w  à vel. Angular =w=v/r = (1500 ft/s)/(0.4590 ft) =3,267.86 rad/s

b) θf= θi + ½(wi +Wf) t

θf = 0 + ½ (0 + 3,267.86) (0.0006s)

θf =0.98 rad

Proyecto Mapas Conceptuales

estos temas son referentes a los mapas conceptuales de la semana 12 a 18 de octubre

una disculpa por haberla subida hasta este momento

por que estuve enfermo pero aqui estan mis mapas conceptuales

si los archivos no son previsualizados en este lugar se encuentran en la parte de galerias

Comentario Leyes Newton

En este blog de esta semana veremos y comentaremos sobre la Dinamica  vistas desde un punto de vista de una pagina conocida.

Los temas a ver son los siguientes:

– Fuerzas y Acciones.

– Leyes de Newton.

– Fuerzas de Rozamiento.

– Sistemas no Inerciales.

– Laboratorio de Dinamica.

– Laboratorio de Rozamiento.

Esos son algunos de los temas q veremos para comenzar nuestra exploracion del tema en esta pagina, asi, sabiendo los temas, podremos dar nuestra opinion de cada uno de ellos. haciendo incapie de nuevo, que la informacion esta en una pagina ya conocida, solo daremos un comentario de ellos, no se copiara la informacion.

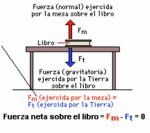
En el tema de la fuerza y accion nos da como primera informacion la definicion y algunas de las formulas de la cinematica y de dinamica, dandonos unos ejemplos de un objeto como se ejerce una velocidad dandole movimiento.

Entre mas sea el impulso q se le da al cuerpo, la velocidad sera mayor, a eso se le conoce como fuerza. cuando un cuerpo de tiene una velocidad y se le da mas impulso se crea una aceleracion. Puede suceder que se aplique una fuerza y la velocidad sea constante sin cambiar, si la fuerza es  perpendicular a la direccion de la velocidad varia su direccion y si la fuerza es inversamente al cuadrado de la distancia al punto se crea un eclipse. La masa es un factor muy importante a considerarse en la fuerza sin la masa no podriamos calcular la fuerza.

Tambien nos dice los comienzos en una sintetizada parte de las tres leyes de Newton.

Nos da algunos ejemplos de la ley de la Inercia, cuando un cuerpo no actua ninguna fuerza, su resultante es nula, mientras un cuerpo tenga fuerza aplicada tendra una velocidad constante.

Reposo movimiento rectilineo y uniforme son son equivalentes.

Tambien nos dice de los princicios de la relatividad nos dice q un cuerpo en movimiento, por poco que parezca, produce un movimiento por la gravedad dada y el peso con la velocidad en que este un objeto.

Nos dice tambien sobre la segunda ley de Newton y nos dice que es una Fuerza resultante donde dichar fuerza nos da una masa y la aceleracion para poder calcularla. La unidad de una fuerza esta calculada en Newtons segun el SI.

La tercera ley de Newton nos dice que para toda accion hay una accion, que qiere decir si un cuerpo ejerce una fuerza sobre otro el otro la ejercera sobre ese mismo.

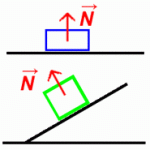
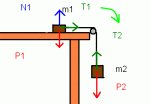
La fuerza de rozamiento surge cuando a un cuerpo se le aplica fuerza sin haber deslizamiento se da una friccion y se da la fuerza de rozamiento estatico, y aplicando a otro cuerpo fuerza deslizandolo se da la fuerza de rozamiento cinetica.

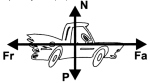
Sistemas no Inerciales, nos dice que si un cuerpo que es estatico esta sobre otro que no lo es, si los cuerpos sufren de un movimiento dado por la velocidad, este cuerpo q esta en movimiento ira en contra del movimiento y se ira hacia el otro lado en direccion contraria. Tambien nos dan algunos eejmplos y problemas donde vienen estas formulas implementadas donde una de ellas es la de la fuerza centrifuga, nos dice que para poder darse una fuerza centrifuga es muy necesaria la gravedad y la aceleracion del cuerpo tambien como su peso.

Nos da a conocer, de igual manera la Mecanica Newtoniana, que esta basada en la idea de un tiempo absoluto y de un espacio tambien absoluto. Nos dice q las primeras investigaciones para llegar a esta ley fue de Maxwel en 1890 con su teoria Electromagnetismo y Einstein en 1905 con la Relatividad.

En los laboratorios podemos encontrar unas herramientas que nos serviran para poder hacer calculos facilitandonos problemas y algunas ecuaciones.

Por mi parte, me parecio muy interesante esta pagina, ya que nos da muchas herramientas y podemos utilizarlas.

Ensayo correspondiente a las Leyes de Newton

Para empezar a hablar sobre las leyes de Newton empezaremos con una breve introduccion de quien es Isaac Newton

Isaac Newton fue un gran científico, de hecho es considerado por muchos como el mayor científico de la Historia. Si bien la mayor parte de sus escritos tratan de religión y alquimia, su contribución en las Matemáticas y la Física es enorme. Sentó las bases de una rama matemática, el Cálculo, y publicó la que se considera una de las obra científica más importantes de la historia, Philosophiae Naturalis Principia Mathematica (Principios matemáticos aplicados a la Filosofía natural, se suele denominar los Principia).

En los Principia, Newton define gran cantidad de conceptos claves en Física, como materia o fuerza y también enuncia las tres leyes de la dinámica, aunque él lo hace como principios. Estas leyes son la base de la mecánica newtoniana (hay distintas mecánicas, según los métodos que se usen en ellas, aunque, obviamente, aplicadas a los mismos problemas todas dan los mismos resultados), y son realmente intuitivas, aunque tal vez esta opinión no sea muy objetiva.

Por comienzos de sus leyes, veremos la que es la primera ley de Newton.

Ley de la Inercia, viene a decir que si dejamos las cosas tranquilas o estaticas en un lugar sin movimiento no habra ningun cambio en como se muevan y si llegaran a tener movimiento en linea recta a una velocidad constante o determinada seguiran igual. Tambien hay que recordar q la velocidad es un vector, es decir, que si cambia la direccion en la que se mueve el objeto, aunque recorra las mismas distancias en el mismo tiempo es un cambio de velocidad. Al no dejarlas sin movimiento es aplicarles fuerza.

Ley de la la fuerza, donde nos explica como varian las propiedades del cuerpo al aplicarle fuerza, o visto desde otra manera es la definicion de la fuerza. Se puede decir que la variacion en el tiempo del momento es la fuerza. Si se supone que la masa no varia, esta variacion respecto al tiempo es de la velocidad, y la variacion de la velocidad respercto al tiempo es la aceleracion. Es por ello que se dice que la fuerza es el producto de la masa por la aceleracion.

Ley de accion y reaccion, es la mas facil de entender, es la cumplable de que cuanto mas fuerte sea el golpe, mas duele. A toda causa, hay un efecto, un ejemplo claro seria al apoyarnos en el suelo, nosotros aplicamos una fuerza, nuestro contra-peso, es el q nos hace sentir la gravedad hacia el suelo, el cual nos hace sentir un peso mucho mayor.

Si esa fuerza no existiera, o no fuera tan intensa que nuestro peso , saldriamos volando o nos humndiriamos en el suelo.

Problema:

Un amigo y tú tiráis, con una fuerza de 500N, de una embarcación situada en el centro de un canal de 20 m de ancho, desde cada lado del mismo y por medio de dos cuerdas unidas a la proa. a) ¿Es lo mismo que tiréis desde cerca que desde lejos de la barca? b) ¿Qué ángulo deben formar vuestras fuerzas de 500 N con el río (tirando las dos con igual ángulo) para obtener una fuerza de 800 N sobre la barca? c) ¿Cuál es el factor limitante para llegar al máximo teórico? Nota:- Para resolver el problema y mientras lo memorizas haz un esquema y anota los datos ya pasados al S.I. Sólo si conoces bien la historia planteada tu cerebro puede sugerirte soluciones. Si un amigo te plantea un problema personal ¿podrás aconsejarlo sin haber conocido, memorizado y razonado sobre todas las circunstancias?

Resolución problema 1
a) Descomponemos la fuerza de arrastre en dos componentes: una perpendicular (Fy) y otra en la dirección del río (Fx).
Al alejarte de la barca el ángulo que forma la fuerza de arrastre es menor y la componente de arrastre (Fx) se hace mayor porque los cosenos de ángulos próximos a 0º tienen valores cercanos a 1, y los de ángulos próximos a 90º están cercanos a 0.
Por lo tanto cuanto más lejos de la barca tires mayor es tu componente de arrastre en la dirección del río.

b) 2 • F • cos (ángulo) = 800
2 • 500 • cos (ángulo) = 800
cos (ángulo) = 800/1000
ángulo = 36,8º = 36º 52′ 11»

c) A medida que se hace menor el ángulo va aumentando la componente de tu fuerza en la dirección de la tracción (Fx), pero tambien es mayor la longitud de la cuerda que tienes que arrastrar. Aunque en este problema no se considera este factor si debe ser tenido en cuenta porque una parte de tu fuerza se emplea en mantener tensa la cuerda venciendo su peso, por lo que aparece otra componente de tu fuerza hacia abajo y sólo queda una parte de ella en el plano horizontal de la barca.
Por lo tanto, tirar desde más lejos supone una mayor componente Fx, pero es necesario emplear una parte mayor de la fuerza en arrastrar la gran cantidad de cuerda utilizada.

ceti

Bienvenidos al Blog hecho para estudiantes del CETI para darse cuenta de los trabajos realizados por mi, les doy las gracias por entrar a vernos y no se olviden entrar a las subcategorias de las materias